次回は、第5期最終回で、論理パズルの難問をお届けします。 もちろん、早解きできる方はしてくださって全く差し支えありませんが、僕自身 としては、週末に時間をじっくりかけて解くイメージを想定した出題です。 ですから、最初わかりにくいからと言って、早々と諦めてしまわない 虫食い算なのですが、解き方からわかりません。 このような問題です 問題1 今日は、平成21年(西暦09年)11月14日です。これにちなんで、次の問1、問2の計算が正しくなるように、 に数字(0,1,2,,9)を書き入れなさい。 〔問1〕 09 14/7/ 心に強く訴える 虫食い算 割り算 難問 孤独の7 虫食い算 スタンの算数教室 次の虫食い算の解き方を教えてください c dが7と97/6/21 お子さんの学年に合わせてステップを上げていくと効果的です。ただし割り算の虫食い算は中学入試でも使われることもあり、低学年で解けなければ
1
虫食い算 難問 解き方
虫食い算 難問 解き方- 算数が苦手な生徒の中に<虫食い算>にまったく手が出ない子がいます。 解き方を覚えれば1つ多く丸を取れるのに、これはもったいない。 と言う訳で今日は<虫食い算>の解き方を取り上げます。 雙葉の1998年(平成10年) と 明大明治の15年(平成27年) です。旅人算の解き方 図形が動いた跡の面積の求め方 てんびん図を使う食塩水問題の解き方 過不足算の公式と図解 1 展開図で見つける立方体の頂点 三角定規の性質と活用法




50 虫食い算 割り算 難問 虫食い算 割り算 難問 Josspix00ux
また、「 算の逆算は 算」という覚え方もありますが、これは良くありません。 なぜなら、引き算・割り算の逆算は一種類の公式にできないからです。 それに配慮してか、親切なテキストでは、抽象的な記号を使った公式が載っていることもありますが 逆算の公式(一部) 足し 僕なりに逆算(虫食い算)の解き方を、解説してみようと思います。 リンク 逆算の解き方 基本は3ステップです。 手順1まずは計算の順序を考えてみましょう。 逆算ではなく、普通の計算の順序で、+-×÷に番号を付けます。 手順2 流水算が苦手をなくす解き方&教え方のコツは意外と簡単! ポイント①流水算特有の用語や小学生が聞き慣れない言葉を理解しよう 流水算では普段聞き慣れない用語や聞いたことはあってもはっきりと分からない言葉があります。 まず流水算を解けるようにするためには言葉の意味を
8月 05, 21 虫食いひき算 小三 ①次のような、虫食いひき算の枠を提示します。 ルールは、 の中に、0から9までのどの数を入れてもOK、というールで同じ数を何回使ってもよし、筆算を完成させます 虫食い算を解くときには今書いた①、②の順番を逆から計算していく ②170ー①⬜︎=1 そうすると①と書いた⬜︎は170ー1で169となりますね。 ①⬜︎が169だとわかったので ①13×⬜︎=169 つまり、169÷13=13となる。 どこから解いたらいいのかわからなく中学受験算数を、わかりやすい、やさしい動画で教えます! 今回は、虫食い算について説明します! チャンネル登録はこちらから https//wwwyoutube
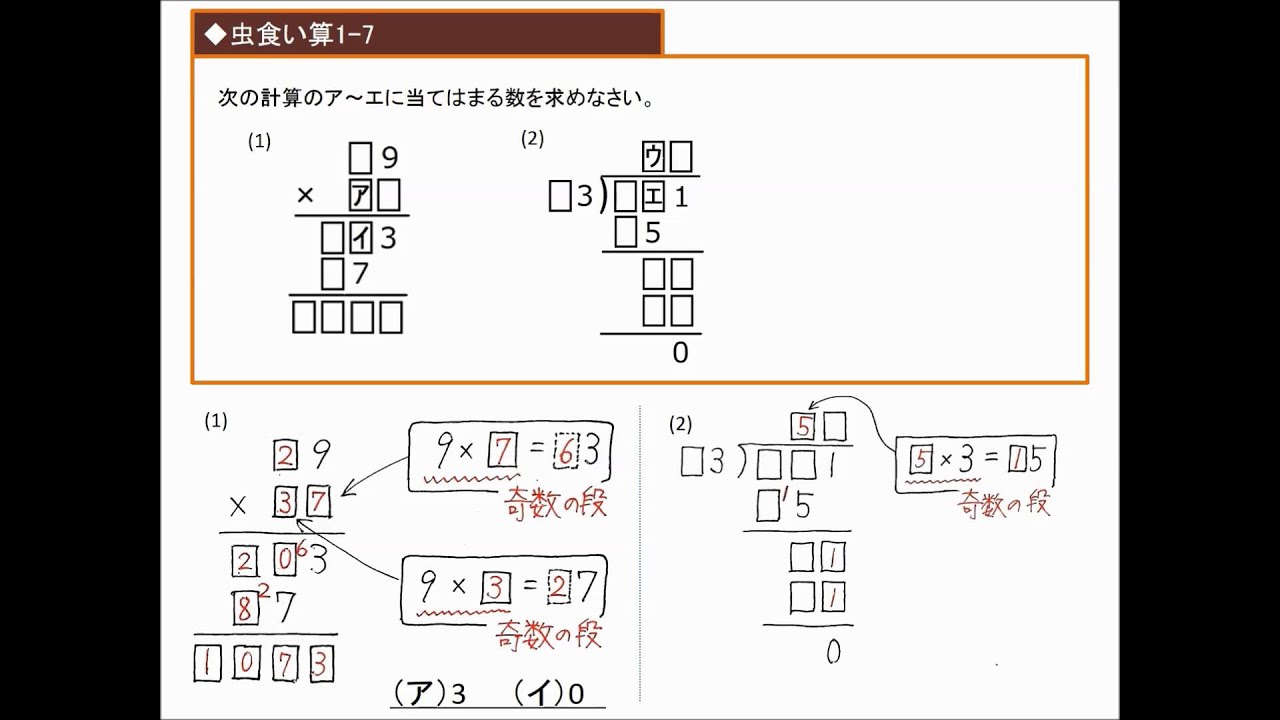
かけ算の虫食い算の基本的な考え方(2) やはり1段で、こんどは の数をちょい増やしてみました。基本的な考え方は(1)とほぼ同じですが、慣れていただくためですかね。 イは偶数。イ×3の一の位が4になるのは、イが 8 の時。 4 で、ウは 1 。念のため、 ・例題:その5_ 虫食い算のかけ算 次覆面算の解き方ヒント 桁の繰り上がりに注目 各位の計算を式にして、これらを満たすように 表を使って当てはまる数を調べる。 その他の工夫 同じ形の枠を用意する 使用文字一覧を作る 残り数字チェックを常にする アルファベットを利用する 最大・最小・奇数・偶数に注意 上下入れ替え 同�このように、小学生の虫食い算は、時系列を遡って行きながら解きます。 移行 さて、この問題を「移項」して解きなさい、と教える人がたくさんいます。 ( ) × 4 5 2 = 15 ( ) × 4 = 15 5 2 ( ) = 12 / 4 = 3 中学生以降に数学を習うと、このように機械的に




小学生虫食い算です 解き方教えて下さい 12 5 27 2 には 数学 教えて Goo



Spi非言語問題 虫食い算 の解き方 就活の答え
覆面算を解くときにはいくつか必要なものがあります。 十分な大きさの紙面 (かなりごちゃごちゃするので、スペースに余裕があると良いです) 鉛筆、ボールペンなど (2色以上あるとなお良い) 覆面算を解くときは次のような流れで解くことが多いです割り算の筆算の虫食い算が分かりません上が問題で下が答えです やり方が分からな Yahoo 知恵袋 美しい 虫食い算 割り算 難問 中学3年数学 2次方程式の利用 文章題part3 Youtube 方程式の解き方 2次方程式の重解について 受験数学って暗記 仮 高校受験 大学受験虫食い算に「簡単な解き方」は、ない 超難問の虫食い算ご教授お願いします! ととのいました。 12 として、÷=!!内訳あたり計算で、 34=× として、106×=**÷=***と仮定し普通の割り算(縦式)で書きながら3回補正したらでました。心に強く訴える 虫食い算 割り算 難問 孤独の7 虫食い算 スタンの算数教室



こちらの虫食い算の解き方を教えてください 10の位から1借りて12 Yahoo 知恵袋



3
Tue SPI非言語問題: 「条件と領域」問題の解き方 Mon SPI非言語問題: 「虫食い算」の解き方 Mon SPI非言語問題: 「重複順列・重複組み合わせ・円順列」の問題 Mon SPI非言語問題: 「整数の推測」問題の解き方 Sun数詞覆面算(作者不明 上と同じAウェイン氏の作と考えられる *1 )() 京都・大阪・東京(森本清吾氏作)() 混合算 ファインマンの問題(W F Cheney, Jr氏作)() 注 *1上の数詞覆面算の解答が発表されたときに、編集者が紹介している。 心に強く訴える 虫食い算 割り算 難問 孤独の7 虫食い算 スタンの算数教室 楽天ブログ 次の虫食い算の解き方を教えてください c dが7と9までは理解したの小学生の割り算の問題プリントを作りました。 単元・内容ごとに順を追って、または、やりたい内容を



虫食い算の簡単な解き方は 下の問題は割と簡単に解けましたが 答え Yahoo 知恵袋



2
虫食い算 難問 1298虫食い算 難問 4桁 リンクを取得 ; 虫食い算に「簡単な解き方」は、ないです。 いわゆる難関私立中学の受験で 虫食い算が積極的に出題されるのは 「決まった手順で解ける問題しかできない子は、 ウチにはいらない。」 と学校の側が考えているからで ある意味、 「こう考えれば解けるよね」 「ここに気が付かないと解けない 虫食い算の解き方について 虫食い算の解き方がわからず困っています。解説に解き方が載っていなく解けません 解ける方がいましたら宜しくお願いします 途中計算の記載も大変だとは思います がお願いします ①52 ×3=2 ②( -629)×32-35=925




虫食い算 筆算工房こつこつ



2
これを虫食い算の普通の(?)解き方で解くと得意な方でもかなり苦労する のではないでしょうか。 しかし、やはり紙とえんぴつでいろいろ考えながら解くことに虫食い算の 面白さがあると思いますが... この本には虫食い算だけでなく覆面算等を含めて1321−7.油分け算 油等を与えられた容器だけを用いて等分する問題が、「油分け算」である。 吉田光由の著した『塵劫記』(寛永8年版、1631) 1 に、こんな問題がある。 「斗桶に油が1斗(=10升)ある。 これ二人で分けるのだが、7升ますと3升ますしか虫食い算の解き方 ア、イ、ウにあてはまる数は? (桜蔭中学 受験算数問題 09年) どうやって計算する? (栄東中学、東大クラス選抜 10年算数入試問題) 当てはまる数は? (桜蔭中学 09年) AとBにはどんな数字が入る? (中学受験算数 数の



1




3年生 かけ算のきまり 虫食い算 Youtube
教科書 3年 unit 311 虫食い算の基本 足し算、引き算、かけ算の虫食い算 例題と解説 トレーニング 確認テスト ログインが必要です フィードバック (不具合・誤記・問題解法の矛盾に関する連絡) ご利用頂きまして誠にありがとうございます。 ご記入頂い国語販売教材 サンプルページ ・その3_虫食い算・足し算の基本(2) 4年 虫食い 虫食い算 解き方をお願いします! 数学 spiの問題について(虫食い算) 問4ケタのabcdがあり、下の二つの条件①・②が成り立つとき、a・b・c・dの整数の合計はいくらか。 ① abcd cdab 2 1 7 8 ② ab=cd×21 答①式を見ると2桁目で計算が分かれていることに気が付く。ab>cdより、cdab




Amazon Fr 続受験算数の裏ワザテクニック 新装版 Tadashi Yamauchi Livres



虫食い算 中学受験ー算数解き方ポータル
主な解き方 方針 割る数を絞り込んで行く。 例 4桁3桁の部分の1000の位は1である。 解答 佐野昌一 『虫喰い算大会』:新字新仮名 青空文庫 の例題七を参照 。 下平和夫「vii 数学特論、3 興味ある数学問題、§33 虫食い算」『新数学事典』を参照 。 考え方の順序と解法例はこちらで!下のファミリーページにもどうぞ! ↓ 問題+解法のセット集→「算数解き方ポータル」 どう解く?中学受験算数 パズルのような算数クイズ 算数オリンピック問題に挑戦! 全国170中学校の入試問題と解法学ぶ・教える.COM > 中学受験 > 算数 > 虫食い算 > 基本問題4 > 解答 講座・問題集 (解答) 1×3 = 4となるのは3 (除数)が34のとき。 1×34=34 2×34=68 余りは0なので、12×34=408より、問題は408÷34であり、残りの は通常のわり算で求められる。 ← 問題に戻る 次の問題 → 相互リンク登録 利




Spi非言語問題 虫食い算 の解き方 就活の答え




数の大きさ 感覚を磨く 孤独の7 竹内洋人 マナビレンジャー 合格への道 中学受験サポート 教育 受験 就活 読売新聞オンライン
一番 印象に残っているプログラムが、虫食い算 の中で、更に自分自身を呼び出す、という、プログラミングの醍醐味を味わえる作り方だ。 虫食い算とは、数字の部分が虫に食われて判明出来ず、残された文字を手掛かりに 全体を復元する、というパズルで、 掛け算の数字が虫食いになった



ざがあとたうん はずかしブログ 小学校4年生の問題



虫食い算 虫食算 学ぶ 教える com



最も選択された 虫食い算 1から9 掛け算 シモネタ



虫食い算です どなたか解き方 答えを教えてください ここまで埋まっていない Yahoo 知恵袋




算数的分野 虫食い算の完成




50 虫食い算 割り算 難問 虫食い算 割り算 難問 Josspix00ux




50 虫食い算 割り算 難問 虫食い算 割り算 難問 Josspix00ux




家電 修理 部品 メーカー直仕入れ 純正 新品 シャープ 背面 Aquos レコーダー 冷却 数量は多 ファン



50 虫食い算 割り算 難問 虫食い算 割り算 難問 Josspix00ux



孤独の7の答え




難問 人気記事 一般 アメーバブログ アメブロ
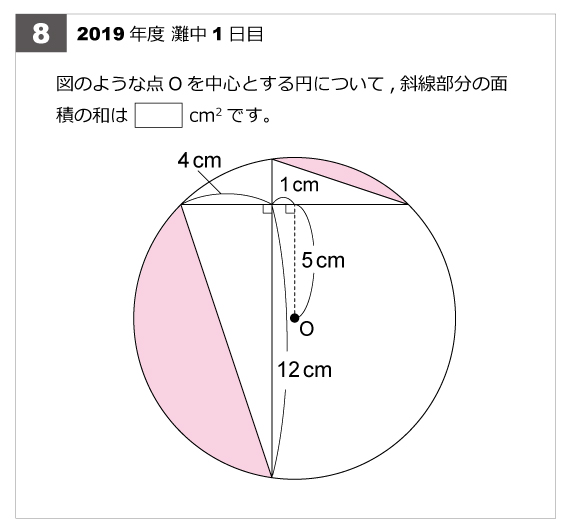



第8問 円の中の図形19年第8問 円の中の図形 算数星人のweb問題集 中学受験算数の問題に挑戦




N E9 80 B2 E6 95 Twitter Search



和算において 鶴亀算とは どういうものでしょうか Quora



綺麗な虫食い算 楽しいクイズの発信基地 クイズ大陸




数の大きさ 感覚を磨く 孤独の7 竹内洋人 マナビレンジャー 合格への道 中学受験サポート 教育 受験 就活 読売新聞オンライン



虫食い算 難しい
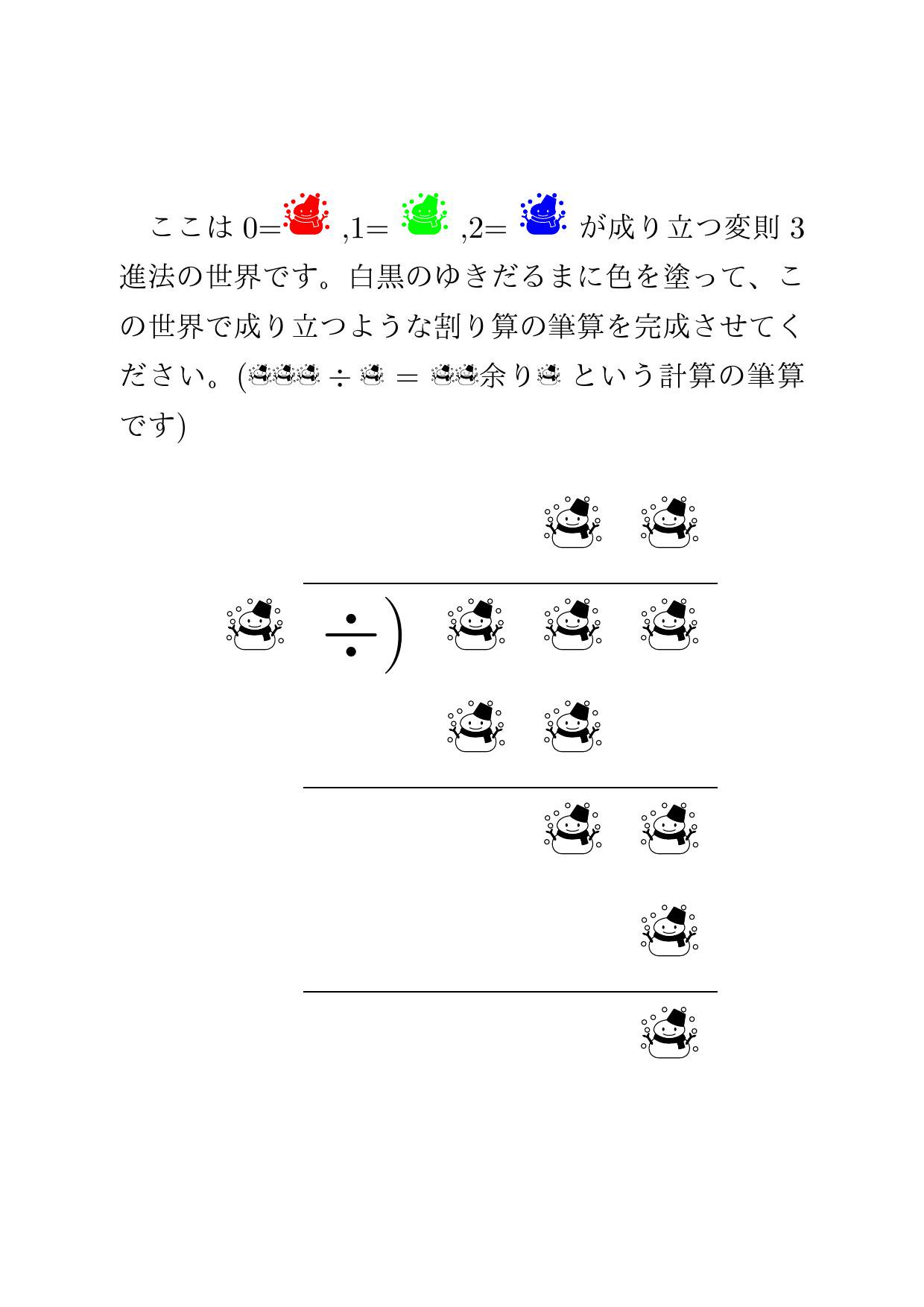



N進法 Twitter Search Twitter




子どもに大ウケ 虫食い算 の算数ゲーム4選 みんなの教育技術




中1が作った激ムズ虫食い割り算 穴だらけだが答えはひとつになる良問 ライブドアニュース



2




覆面算 有名な問題 Send More Money もっとお金をよこせ Jyankquiz



2015年 四天王寺中学 虫食い算から パズル算数クイズ




こうして学べば必ずわかる 中学受験 理科




最高のコレクション 虫食い算 割り算 47 虫食い算 割り算 難問 Mbaheblogjpbtco




World Mastermind 帽子 バケットハット メンズ Mastermind ハット マスターマインド Hat メンズ Logo 帽子 Logo Bucket Black フェルマートマスターマインド 帽子 ハット Black サイズ交換無料 大人気の新品登場



2




虫食い算 筆算工房こつこつ




虫食い算のレベル別攻略法 駒澤塾 中学受験の算数 理科




虫食算 孤独の7 の解法 ニコニコ動画




ナンプレ1 問の中古 未使用品 メルカリ
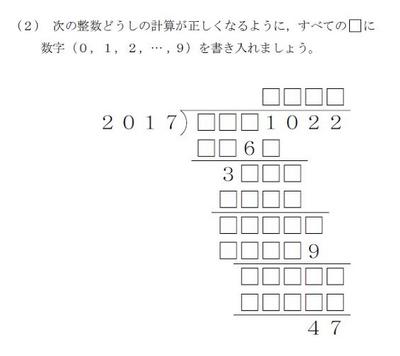



醸芳小学校 桑折町教育ポータル



1 0 624 37 の虫食い算のやり方教えてください 宜しくお願 Yahoo 知恵袋



逆算の解き方 カテキョウブログ




虫食い算 筆算工房こつこつ



筆算の虫食い算ドリル




ワタナベオイスター 渡辺オイスター 天眼 漢方相談店 即納送料無料 税込み3980円以上送料無料 医薬部外品 70ml たんぽぽ薬房 株式会社メニコンエピカアクアモアクリア



割り算の筆算の虫食い算が分かりません上が問題で下が答えです やり方が分からな Yahoo 知恵袋



1




虫食い 算 足し算 解き方 マインクラフト Ps3 ダウンロード




覆面算を解くテクニック集 カナンの数学ノート




フィボナッチ数列 最上級問題 フィボナッチ数列 算数星人のweb問題集 中学受験算数の問題に挑戦




自宅で受講できる 私国立中学入試対策 難関選抜ゼミ



ファインマンの手紙 の虫食い算



けっこう難問かも 算数クイズ その14 脳トレ 脳幹を64倍活性化



足し算の虫食い算です パズル算数クイズ



2




全国180中学の入試算数 解法研究



クイズ大百科事典 820問があなたに挑戦




中1が作った激ムズ虫食い割り算 穴だらけだが答えはひとつになる良問 ライブドアニュース




合計数を手がかりに数字を入れていくパズル カックロ の大判です まんぞくカックロ Bookウォッチ




逆算の解き方 カテキョウブログ




小学校の算数で登場する魔方陣の解き方を丁寧に解説します 数学の面白いこと 役に立つことをまとめたサイト




算数オリンピック12 トライアル 虫食い算 解説 Youtube



逆算の解き方 カテキョウブログ



1 0 624 37 の虫食い算のやり方教えてください 宜しくお願 Yahoo 知恵袋



虫食い算1 7 中学受験 算数 小4レベル Youtube




科学雑誌newton ニュートン 虫食い算 ってご存じですか ある数式の一部分が でかくされていて そこに入る数字を考える定番パズルです 下は オドリングの孤独の7 とよばれる虫食い算の名作かつ超難問です いくら何でも虫食い過ぎですね 一見 手がかり




私立国立中学入試対策 算数の極意 メルカリ




のどのあれ 痛み 口中殺菌 新作 大人気 口臭除去に 指定医薬部外品 ノドニトローチ 3個セット 皇漢堂製薬 24個



私立中学 入試 問題の難問 偶然に 正解 セルフ塾のブログ




覆面算を解くテクニック集 カナンの数学ノート




中1が作った激ムズ虫食い割り算 穴だらけだが答えはひとつになる良問 ライブドアニュース




虫食い算 筆算工房こつこつ




Amazon Fr 続受験算数の裏ワザテクニック 新装版 Tadashi Yamauchi Livres



簡単な虫食い算ですが 論理的に解いてみましょう 07 09 17 学習塾ロジム 今週の1問



虫食い算 中学受験ー算数解き方ポータル



この筆算を完成させて 2004年ジュニア算数オリンピック トライアル問題より 算数オリンピック問題に挑戦




オフィスに最適な国産システム収納庫 完成品 組立不要 オンライン限定商品 国産 日本製 オフィス家具 クウォール システム収納庫 片開き書庫 鍵付き キャビネット スチール書庫 Rw5 18h45ファイル 収納 Quwall 書棚 本棚 幅450mmタイプ 高さ1800mm



虫食い算 パズル算数クイズ




最高のコレクション 虫食い算 割り算 47 虫食い算 割り算 難問 Mbaheblogjpbtco




最高のコレクション 虫食い算 割り算 47 虫食い算 割り算 難問 Mbaheblogjpbtco



これも虫食い算の一種かな 麻布中学 2003年 解けるかな 算数の難問に挑戦



2015年 四天王寺中学 虫食い算から 中学受験ー算数解き方ポータル



完了しました 虫食い算 割り算 難問 素晴らしいドラえもん




ほとんど食われた虫食い算 の巻 Youtube




虫食い算 筆算工房こつこつ




難問 人気記事 一般 アメーバブログ アメブロ



ファインマンの手紙 の虫食い算



中1写真の虫食い算の解き方が分かりません 教えていただけると嬉しいです Yahoo 知恵袋



虫食い筆算を完成させて 2011年算数オリンピック トライアル問題から 算数オリンピック問題に挑戦




数の大きさ 感覚を磨く 孤独の7 竹内洋人 マナビレンジャー 合格への道 中学受験サポート 教育 受験 就活 読売新聞オンライン




50 虫食い算 割り算 難問 虫食い算 割り算 難問 Josspix00ux




虫食い算 ハレやか特製脳活パズル Vol 9



最も選択された 虫食い算 1から9 掛け算 シモネタ



三石 数学塾 虫食い算
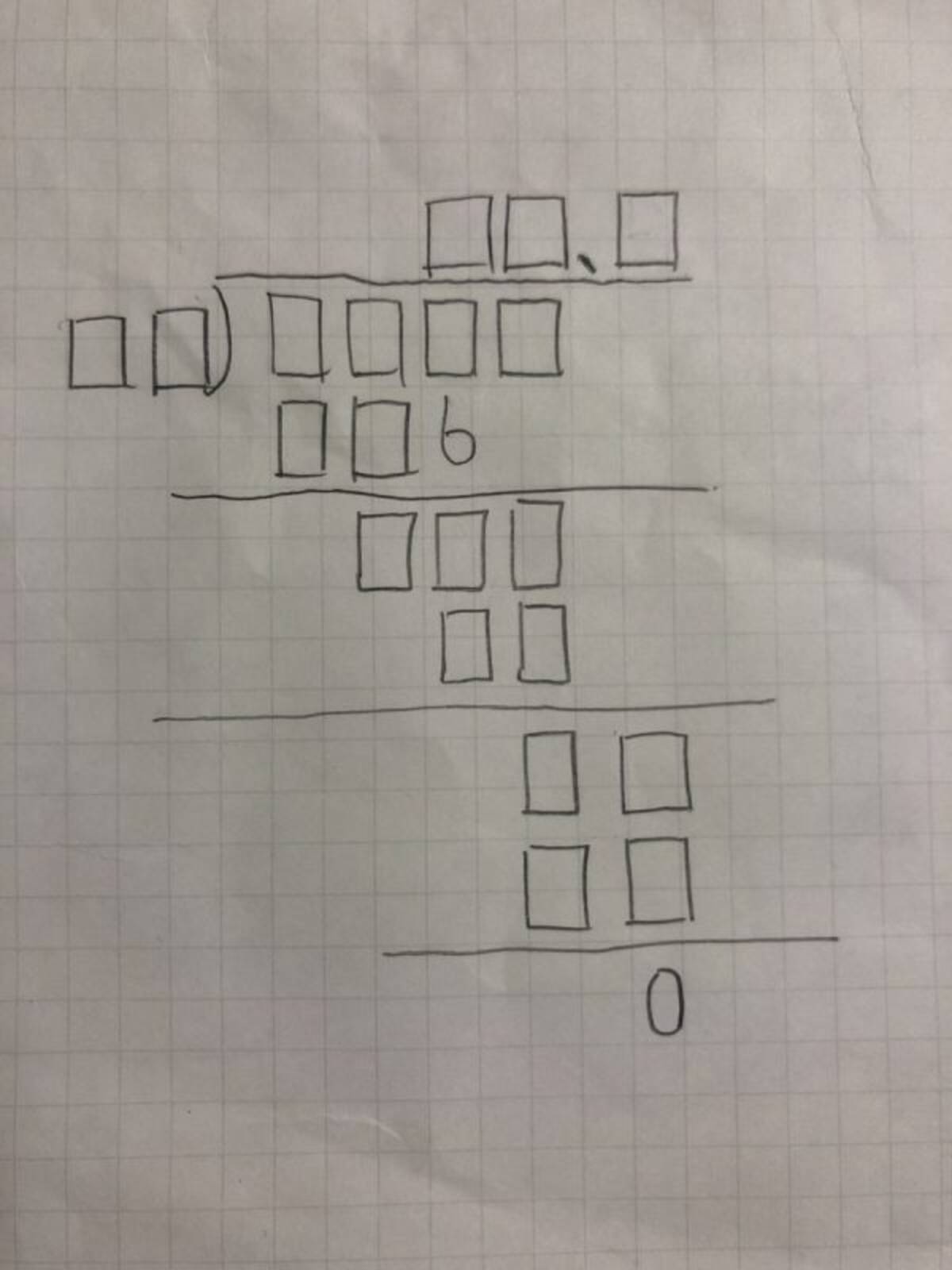



ほとんど全部穴じゃん 中1が作った割り算の 虫食い算 の難易度が激ムズ 年2月7日 エキサイトニュース



虫食い算特集 1 みんなで脳トレブログ 遊びゴコロで 楽しく 脳トレ 石川県金沢市




中学受験算数 虫食い算にチャレンジ 算数パズル問題 面白い問題 2通り目は難問です 四則演算だけで解き方のコツを解説 小町算 覆面算 数学パズルの問題です Youtube




虫食い算1 9 中学受験 算数 小4レベル Youtube



0 件のコメント:
コメントを投稿